José Antonio Zapata
Centro de Ciencias Matemáticas
UNAM Campus Morelia Morelia
CP 58190 Michoacán, México

Antes de estar aquí:
Licenciatura en física UNAM, México
Doctorado en física Penn State, USA
Postdoc RRI, India

Modelos discretos para teorías de campo (incluyendo la gravitación)

Abajo leerán que mi trabajo en investigación comenzó estudiando modelos discretos para la gravitación.

Después de N años, he regresado a los modelos discretos para teorías de campo. Mis nuevas propuestas tienen intenciones muy ambiciosas. Los modelos son locales, covariantes y a la vez gozan de una estructura geométrica que generaliza a la estructura simpléctica de las teorías canónicas.

Multisymplectic effective General Boundary Field Theory
Mona Arjang (mi estudiante de doctorado), Jose A. Zapata, Class.Quant.Grav. 31 (2014) 095013

Un aspecto más del plan al que pertenece este artículo es el concepto de teoría efectiva a una escala dada, el proceso de engrosamiento, el proceso de renormalización de Wilson para la cuantización de lazos y su correspondiente límite continuo. Por eso, dentro del artículo también se estudia una aplicación de engrosamiento.

Más aún, las estructuras que propongo en este trabajo son tales que la cuantización de esta familia de modelos lleva a los llamados modelos de espuma de espín; dándoles a ellos un marco clásico y semiclásico mucho mejor estructurado y apto para abordar preguntas físicamente relevantes.

Una muestra del poder de este formalismo es mi nueva propuesta para estudiar observables físicas dentro de un marco local y covariante usando corrientes observables.
--

Henri Waelbroeck, mi asesor de tesis de licenciatura, propuso una descripción de la gravitación 2+1 dimensional basada en una teoría de gauge sobre la red; una extensión directa de su formalismo en cualquier dimensión conduce a una formulación de la teoría BF sobre la red. El artículo

A Hamiltonian formulation of topological gravity
Henri Waelbroeck, Jose A. Zapata, Class.Quant.Grav. 11 (1994) 989-998

se enfoca en 3+1 dimensiones y tiene los siguientes objetivos:

(i) Provee una imagen geométrica de esta descripción de la teoría BF estudiando soluciones de un conjunto de condiciones en el campo B que implican que existe una forma de soldadura tal que 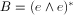. Bautizamos a estas condiciones con el nombre de "condiciones de geometricidad," pero después del éxito del modelo de Barrett y Crane las condiciones se han vuelto conocidas bajo el nombre de "condiciones de simplicidad."

Propone una estrategia para la gravitación en redes (y por consiguiente para la gravitación cuántica).
Comenzando con una formulación de red para la teoría BF, el primer paso identifica condiciones que hacen a la teoría geométrica, 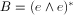, mientras que el segundo paso seleccionan el subgrupo máximo de las simetrías de la teoría BF que preservan las condiciones de geometricidad.

Ahora sabemos que la misma estrategia emerge de discretizaciones de la acción de Plebanski; sin embargo, cuando nuestro trabajo fue publicado la acción de Plebanski para la relatividad general no era tan conocida como es ahora, y nosotros no la conocíamos.

Errata: La formula que usamos para las constantes de estructura del grupo de Lorentz es incorrecta. Sin embargo, nuestros resultados finales son correctos. (El siguiente artículo compone esta errata.)
--

Cuando el espacio de fase del modelo descrito arriba se complexifica, se puede factorizar en sus partes auto-dual y anti auto-dual, donde cada una de esas partes es una copia del espacio fase real. El espacio fase real como subespacio del espacio fase complejo se caracteriza por la condición de que sus elementos cumplen que su parte anti auto-dual es el complejo conjugado de su parte auto-dual. Así que puede usarse variables auto-duales para describir el espacio fase real. Este es el punto de partida del artículo

Topological lattice gravity using selfdual variables
Jose A. Zapata, Class.Quant.Grav. 13 (1996) 2617-2634

En este lenguaje, las condiciones de geometricidad toman la forma familiar de las condiciones de realidad de la formulación cuántica de la relatividad general en términos de variables de Ashtekar, y se resuelven tomando como grados de libertad independientes a la parte auto-dual y determinando a la parte anti auto-dual como su complejo conjugado. Además, la parte local de los generadores de simetría que preservan las condiciones de geometricidad/realidad tienen la forma de las restricciones vectorial y escalar de la formulación de Ashtekar de la relatividad general. El artículo muestra que, dentro de la superficie de restricciones, y hasta primer orden en la curvatura, las restricciones forman un álgebra cerrada. Esto es todo lo necesario para el estudio de la gravitación linearizada al rededor de la solución plana. Por lo tanto, este artículo puede verse como una discretizacion de la formulación de Ashtekar de la relatividad general (linearizada). Para lograr este éxito parcial en la búsqueda de un álgebra de restricciones cerrada la parte no local de los generadores de simetría es esencial.