
José Antonio Zapata
Centro de Ciencias
Matemáticas
UNAM Campus Morelia Morelia
CP 58190 Michoacán, México

Before being here:
Bs Physics UNAM, México
PhD Physics Penn State, USA
Postdoc RRI, India
Discrete models for gravity
Henri Waelbroeck, my BSc thesis supervisor, proposed a lattice gauge theory description of 2+1 gravity; a direct extension of his formalism leads to a hamiltonian lattice formulation of BF theory in any dimension. The article
A Hamiltonian formulation of topological gravity
Henri Waelbroeck, Jose A. Zapata,
Class.Quant.Grav. 11 (1994) 989-998
focusses on 3+1 dimensions and achieves two goals:
(i) It describes conditions that allow for a geometrical understanding of
this lattice description of BF theory by studying the solutions of a set of
conditions on the B field that imply that there is a soldering one form such
that 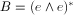 . We called these conditions geometricity conditions,
but after the success of the Barrett-Crane model they have become widely known
as simplicity conditions.
. We called these conditions geometricity conditions,
but after the success of the Barrett-Crane model they have become widely known
as simplicity conditions.
(ii) It proposes a strategy for lattice gravity (and ultimately for quantum
gravity).
Starting with a lattice formulation of BF theory, the first step identifies
the conditions that make the theory geometrical 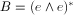 , while the
second step selects the maximal subgroup of symmetries of BF theory that
preserved the conditions.
, while the
second step selects the maximal subgroup of symmetries of BF theory that
preserved the conditions.
Now we know that the same strategy emerges from discretizations of the Plebanski action; however, when our work was published the Plebanski action for general relativity was not as well-known as it is today, and we were not aware of it.
Errata:
There is an errata in the formula that we use for the structure constants of the Lorentz group. However, our final results are correct. (The next article fixes the errata.)
--
When the phase space of the model described above is complexified, it can be factorized into its self and anti self-dual parts, both of these parts being identical copies of the real phase space. Any element if the real phase space can be described inside the complex phase space by the condition that its anti self-dual part is the complex conjugate of its self-dual part. Thus, one can use self-dual variables to describe the real phase space. This is the starting point of the article
Topological lattice gravity using selfdual variables
Jose A. Zapata,
Class.Quant.Grav. 13 (1996) 2617-2634
In this language, the geometricity conditions take the familiar form of the reality conditions of canonical general relativity in terms of Ashtekar's variables and are solved by keeping only the self dual part of the variables. Additionally, the local part of the symmetry generators that preserve the geometricity/reality conditions have the form of the vector and scalar constraints of Ashtekar's formulation of general relativity. The article shows that on shell, and up to first order in the curvature, the symmetry generators form a closed algebra. This would be all that is needed for a study of linearized gravity around a flat solution. Thus, this article can be seen as a discretization of Ashtekar's formulation of (linearized) general relativity. For this partial success in finding a closed constraint algebra the non local part of the symmetry generators is essential.

